Huffman问题

我们都知道哈夫曼树在构造的过程中每一步都是找到两个权值最小的点进行合并。下面根据一道经典问题来进行简单的证明。

例题

合并果子

分析

假设有五个果子a，b，c，d，e。无论以什么样的方式进行合并都可以转化成以一个二叉树，所以能画出很多很多的二叉树，因为有很多的合并方式。那么如何确定最优解呢？

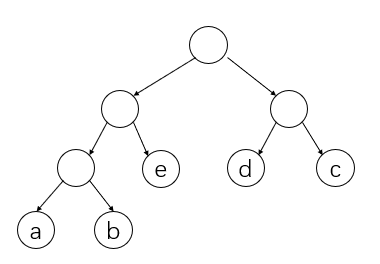
画一种合并方式的二叉树：

第一点：权值最小的两个点一定是在最下面一层，且可以为兄弟节点。 >证明：假设a，b是权值最小的两个点，用反证法，若a不在最下面一层，例如a与e互换，3e+2a一定大于3a+2e，则最后合并的值必然变大，所以最优解中a，b必然在最下面一层。

第二点：f(n)代表合并n个点的最小值，则合并完一个点之后变成了n-1个点也就f(n-1)，而f(n)=f(n-1)+a+b，所以n个点的哈夫曼问题与n-1个点的哈夫曼问题同时取得最小值，然后依次往上递推直到只有一个点。

C++代码

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>

using namespace std;

const int N = 10010;

int n;
int w[N];

int main()
{
    scanf("%d", &n);
    priority_queue<int, vector<int>, greater<int>> q;
    for (int i = 0; i < n; i++) scanf("%d", &w[i]), q.push(w[i]);
    
    int res = 0;
    while (q.size() > 1)
    {
        int x = q.top(); q.pop();
        int y = q.top(); q.pop();
        q.push(x + y);
        res += x + y;
    }
        
    printf("%d", res);
    
    return 0;
}

Java代码

import java.util.Scanner;
import java.util.PriorityQueue;

public class Main {
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        int n = scan.nextInt();
        PriorityQueue<Integer> minHeap = new PriorityQueue<Integer>();
        for (int i = 0; i < n; i++) {
            minHeap.add(scan.nextInt());
        }
        int res = 0;
        while (minHeap.size() > 1) {
            int a = minHeap.poll();
            int b = minHeap.poll();
            minHeap.add(a + b);
            res += a + b;
        } 
        System.out.println(res);
    }
}

习题

题目描述

众所周知的，小明家里有好多猫，经过一次“猫口普查”，我们得到了以下信息：小明家里有n只猫，第i只猫的体重是ai。然而小明热爱虐猫（并不），他决定对这些猫做一些有趣的事情经过了两年半的练习之后，这些猫已经能完全听懂小明的指令了。

小明的指令分成两个阶段，具体步骤如下：

1.指定一种颜色，所有这种颜色的猫都会从猫窝里跑出来，此时小明需要付出总共为这些猫的体重的代价。例如，现在小明有三只红色的猫，体重分别为1，2，3，还有两只蓝色的猫，体重分别为7，8。此时如果小明声明的颜色是红色，那么所有红色的猫会出来，小明需要支付的代价为6。如果小明声明的颜色是蓝色，那么所有蓝色的猫会出来，小明需要支付的代价为15。

2.对于现在出来的这些猫，小明选择其中的一部分，将他们染成一种新的颜色。然后放回所有的猫。初始时所有猫都是白色。现在小明想知道，如果想要使得这些猫两两颜色都不同，最少需要花费多少代价。

分析

这就是合并果子问题的变形，相当于有一堆果子，怎样拆能消耗的体力最小？因为每拆一次就可以把猫弄成两种颜色，直到每一部分只有一只猫。

其实代码和合并果子一模一样。

C++代码

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>

using namespace std;

const int N = 100010;

int n;
int w[N];

int main()
{
	scanf("%d", &n);
   	priority_queue<int, vector<int>, greater<int>> minHeap;
    for (int i = 0 ; i < n; i++) scanf("%d", &w[i]), minHeap.push(w[i]);
    
    int res = 0;
    while (minHeap.size() > 1) 
    {
        int a = minHeap.top(); minHeap.pop();
        int b = minHeap.top(); minHeap.pop();
        minHeap.push(a + b);
        res += a + b;
    }
    printf("%d", res);
    
    return 0;
}

Java代码

import java.util.Scanner;
import java.util.PriorityQueue;

public class Main {
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        int n = scan.nextInt();
        PriorityQueue<Integer> minHeap = new PriorityQueue<Integer>();
        for (int i = 0; i < n; i++) {
            minHeap.add(scan.nextInt());
        }
        int res = 0;
        while (minHeap.size() > 1) {
            int a = minHeap.poll();
            int b = minHeap.poll();
            minHeap.add(a + b);
            res += a + b;
        } 
        System.out.println(res);
    }
}