n皇后与数独

n皇后问题与数独问题可以说是搜索问题中非常经典的两个问题，因此放到一起总结一下。

n皇后

题目链接

做法

搜每一个格子，每一个格子有放与不放两种情况，按照这种顺序进行搜索。当然也可以按照行的顺序进行搜索。

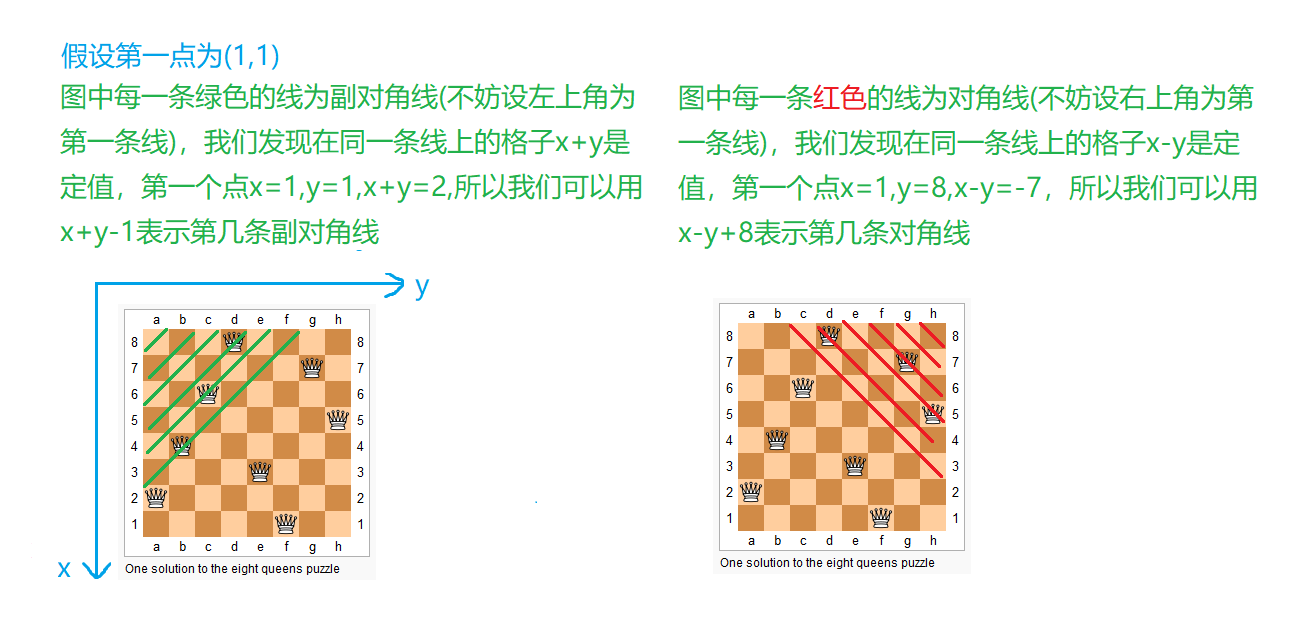
这里介绍一下，对角线与副对角线的表示方式：

C++代码

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 15;

int n;
char g[N][N];
bool r[N], c[N], diag[N * 2], undiag[N * 2]; // 行 列 副对角线 对角线

void dfs(int x, int y, int s) {
    if (s > n) return;
    if (x == n && y == n + 1) {
        if (s == n) {
            for (int i = 1; i <= n; i++) printf("%s\n", g[i] + 1);
            puts("");
        }
        return;
    }
    if (y == n + 1) {
        y = 1;
        x++;
    }
    
    // 这个点不放
    g[x][y] = '.';
    dfs(x, y + 1, s);
    
    // 这个点放
    if (!r[x] && !c[y] && !diag[x + y - 1] && !undiag[n + x - y]) {
        g[x][y] = 'Q';
        r[x] = true;
        c[y] = true;
        diag[x + y - 1] = true;
        undiag[n + x - y] = true;
        dfs(x, y + 1, s + 1);
        // 恢复现场
        r[x] = false;
        c[y] = false;
        diag[x + y - 1] = false;
        undiag[n + x - y] = false;
    }
} 

int main()
{
    scanf("%d", &n);
    
    dfs(1, 1, 0);

    return 0;
}

数独

题目链接

数独好像还有很多优化，位运算？dangcing links？ 算了算了不学了不学了 :(

做法

和n皇后的思路相同，搜每一个位置，每一个位置有两种情况，已经有数或者还没有数，若有数则跳到下一个位置，若没有数则枚举1~9看哪些数满足数独的规则。

Java代码

import java.util.*;
public class Main {
    static int N = 12;
    static char[][] g = new char[N][N];
    static boolean[][] r = new boolean[N][N];
    static boolean[][] c = new boolean[N][N];
    static boolean[][] k = new boolean[N][N];
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        String str = null;
        for (int i = 0; i < 9; i++) {
            str = scan.next();
            g[i] = str.toCharArray();
            for (int j = 0; j < 9; j++) {
                if (g[i][j] != '.') {
                    int num = g[i][j] - '0';
                    r[i][num] = c[j][num] = k[get(i, j)][num] = true;
                }
            }
        }
        // for (int i = 0; i < 9; i++) {
        //     for (int j = 0; j < 9; j++) System.out.print(g[i][j]);
        //     System.out.println();
        // }
        dfs(0, 0);
    }
    public static void dfs(int x, int y) {
        if (y == 9) {
            x++;
            y = 0;
        }
        if (x == 9) {
            for (int i = 0; i < 9; i++) {
                System.out.println(g[i]);
            }
            return;
        }
        if (g[x][y] != '.') {
            dfs(x, y + 1);
            return; // 这里一定不能忘了return    T_T
                    // 因为这里和八皇后问题是不一样的，假如不return就会把原来的数覆盖掉的。
        }
        for (int i = 1; i <= 9; i++) {
            if (!r[x][i] && !c[y][i] && !k[get(x, y)][i]) {
                g[x][y] = (char)(i + '0');
                r[x][i] = c[y][i] = k[get(x, y)][i] = true;
                dfs(x, y + 1);
                r[x][i] = c[y][i] = k[get(x, y)][i] = false;
                g[x][y] = '.';
            }
        }
    }
    public static int get(int x, int y) {
        return 3 * (x / 3) + y / 3 + 1;
    }
}

参考

AcWing笔试面试