CS 61A Fall 2020
2022-10-31 14:20:03 #Python #Awesome Courses
本文总阅读量次

0

推荐顺序：Textbook -> Video -> Lecture's full -> lab and homework

我的代码

Lecture 1 Intro

Lab 00

最后加上--local，例如：python3 ok -q python-basics -u --local，之后所有的测试都加上--local。

Lecture 2 Function

video

https://pythontutor.com/cp/composingprograms.html#mode=edit

Environment Diagrams: 我理解的就是类似于当前所有元素（包括变量，函数，对象等）的集合。

Frame: 运行过程中将name与expression绑定（bound）起来。每一次函数调用都会有一个新的Frame。

HW 01

主要就是这个Q5做的时候一直没看懂是什么意思。经过一番折腾，好在是过了。

要点：

  1. 根据函数with_if_statement和with_if_function的返回值都是None得知，true_func和false_func均无返回值。

  2. 调用with_if_statement和with_if_function时打印出来的东西，也就是说明这两个函数的函数体内有print。

  3. 当函数做函数参数时，无论什么情况都会调用。例子：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    def func(condition, true, false):
        if (condition):
            return true
        else:
            return false

    def condition():
        return True

    def true():
        print('true')

    def false():
        print('false')

    func(condition(), true(), false())

    打印结果：

    1
    2
    true
    false

    注：调用func函数时，传的参数是有括号的，即调用时函数参数condition，true以及false都是函数condition()，true()以及false()的返回值，这样无论condition是否为真都需要调用true()和false()也就不奇怪了。

    补充：调用func函数时，传的参数没有括号，无任何打印。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
# Q2
def a_plus_abs_b(a, b):
    if b >= 0:
        h = add
    else:
        h = sub
    return h(a, b)

# Q3
def two_of_three(x, y, z):
    return x * x + y * y + z * z - max(x, y, z) * max(x, y, z)

# Q4
def largest_factor(x):
    max_factor = 1
    for i in range(1, x):
        if (x % i == 0):
            max_factor = i
    return max_factor

# Q5
def if_function(condition, true_result, false_result):
    if condition:
        return true_result
    else:
        return false_result

def with_if_statement():
    if cond():
        return true_func()
    else:
        return false_func()

def with_if_function():
    return if_function(cond(), true_func(), false_func())

def cond():
    return False

def true_func():
    print(42)

def false_func():
    print(47)   

# Q6
def hailstone(x):
    cnt = 0
    while (True):
        print(x)
        cnt = cnt + 1
        if (x == 1):
            break
        if (x % 2 == 0):
            x //= 2
        else:
            x = x * 3 + 1
    return cnt

Lecture 3 Control

video

python3 -i xx.py

introduce condition statement and iteration.

Lab 01

非0即真，非False即真，非None即真。

Q3: Debugging Quiz! 没好好做，貌似都是关于debug的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
# Q4
def falling(n, k):
    if k == 0:
        return 1
    ans, t = n, n - 1
    for i in range(k - 1):
        ans = ans * t
        t = t - 1
    return ans

# Q5
def sum_digits(y):
    res = 0
    while y > 0:
        d = y % 10
        res = res + d
        y = y // 10
    return res

# Q7
def double_eights(n):
    last = False
    while n > 0:
        d = n % 10
        if last and d == 8:
            return True
        if d == 8:
            last = True
        else:
            last = False
        n = n // 10
    return False

Lecture 4 & 5

Textbook 1.6 Higher-Order Functions

1.6.1 Functions as Arguments

其实就是将函数作为参数：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
def sum(n, term):
    """
    >>> sum(5, natural)
    15
    >>> sum(100, natural)
    5050
    >>> sum(5, square)
    55
    """
    i, ans = 1, 0
    while i <= n:
        i, ans = i + 1, ans + term(i)
    return ans

def natural(k):
    return k

def square(k):
    return k * k

if __name__ = "__main__":
    import doctset
    doctest.testmod()

1.6.2 Functions as General Methods

迭代计算黄金分割率：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
"""
其实就是 y = x 与 y = 1 / x + 1 的交点位置，
即方程 x^2 = x + 1 的解
"""
def improve(update, close, guess = 1):
    """
    update 就是用于迭代猜的值
    close 判断猜的值是否满足精度的要求
    只不过这里的 close 和 update 都是函数罢了
    """
    while not close(guess):
        guess = update(guess)
    return guess

def golden_update(guess):
    return 1 / guess + 1

def golden_approx_eq(guess):
    return approx_eq(guess * guess, 1 + guess)

def approx_eq(x, y, tolerance = 1e-3):  # x 与 y 的差距不超过 tolerance
    return abs(x - y) < tolerance

phi = improve(golden_update, golden_approx_eq)
print(phi)

1.6.3 Defining Functions III: Nested Definitions

在线画函数图像

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
"""
为什么需要 function nested ?
1. global 内函数太多了。
2. update 和 close 应该是某一种计算特有的。
"""
def improve(update, close, guess = 1):
    while not close(guess):
        guess = update(guess)
    return guess

def approx_eq(x, y, tolerance = 1e-3):
    return abs(x - y) < tolerance

def sqrt(a):  # 计算根号a
    def sqrt_update(guess):
        """
        这里采用 (guess + a / guess) / 2 的原因是：
        相当于求 y = x 与 y = (x + a / x) / 2 的交点，
        即方程 2x = x + a / x 的解，显然为根号a。
        不需要关心具体的迭代方法，更需要关注 nest 的好处。
        """
        return (guess + a / guess) / 2
    def sqrt_approx_eq(guess):
        return approx_eq(guess * guess, a)
    return improve(sqrt_update, sqrt_approx_eq)

print(sqrt(256))

1.6.6 Currying

1
2
3
4
5
6
7
8
9
"""
返回值为 function 来实现链式调用
"""
def my_pow(a):
    def f(b):
        return pow(a, b)
    return f

print(my_pow(2)(3))

1.6.8 Abstractions and First-Class Functions

A programming language is said to have First-class functions when functions in that language are treated like any other variable.

1.6.9 Function Decorators

1
2
3
4
5
6
7
8
9
10
11
12
13
def trace1(func):
    def traced(x):
        print('Calling', func, 'on argument', x)
        return func(x)
    return traced

# @trace1
def square(x):
    return x * x

print(trace1(square)(5))

print(square(5))

lab 02

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
# Q1
(lambda: 3)()

b = lambda x: lambda: x
c = b(88)
c()

# Q2
def f1():
    pass
f2 = f1
print(f1 == f2)  # True

# Q3
def lambda_curry2(func):
    return lambda a: lambda b: func(a, b)
# 等价于：
def lambda_curry2(func):
    def func1(a):
        def func2(b):
            return func(a, b)
        return func2
    return func1

# Q4
def count_cond(condition):
    """
    其实无论怎么嵌套，只要记住：
    1. 最内层的 return 是我们想要的结果
    2. 在哪一层 def 就在那一层 return
    """
    def inner_count_cond(n):
        i, count = 1, 0
        while i <= n:
            if condition(n, i):
                count += 1
            i += 1
		return count
    return inner_count_cond

# Q5 Q6 跳过

# Q7
def composite_identity(f, g):
    def inner(x):
        if compose1(f, g)(x) == compose1(g, f)(x):
			return True
        else:
            return False
    return inner

# Q8
def cycle(f1, f2, f3):
    """
    And so far 的意思是，一直往下嵌套下去。
    """
    def func1(n):
        def func2(x):
            if n == 0:
                return x
            elif n == 1:
                return f1(x)
            elif n == 2:
                return f2(f1(x))
            elif n == 3:
                return f3(f2(f1(x)))
            else:
                res = f3(f2(f1(x)))
                i = 4
                while i <= n:
                    if i % 3 == 1:
                        res = f1(res)
                    elif i % 3 == 2:
                        res = f2(res)
                    else:
                        res = f3(res)
                    i += 1
                return res
        return func2
    return func1

Lecture 6 & 7

pass

Lecture 8 & 9

HW 02

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
# Q1
def num_eights(x):
    if x == 0:
        return 0
    return num_eights(x // 10) + (1 if x % 10 == 8 else 0)

# Q2
"""
不能使用赋值语句
"""
def get_direction(n):
    if n == 1:
        return 1
    last = get_direction(n - 1)
    if n % 8 == 0 or num_eights(n) > 0:
        return -last
    return last
def pingpong(n):
    if n == 1:
        return 1
    return pingpong(n - 1) + get_direction(n - 1)

# Q3
def missing_digits(n):
    if n < 10:
        return 0
    b, a = n % 10, n // 10 % 10
    cnt = b - a - 1 if b - a >= 2 else 0
    return missing_digits(n // 10) + cnt

# Q4
"""
Refer Textbook 1.7.5 Example: Partitions
count_partitions(n, m) 为：
	n = a1 * 1 + a2 * 2 + a3 * 3 + ... + am * m
	不同的 a1, a2, ...,am 的数量
count_partitions(n, m) 可以分为两大类：
	1. 包含m：count_partitions(n - m, m)。因为至少有一个 m，我们将这个 m 去掉，也就是在原来 n 的基础上去掉一个 m，即 n - m。同时还是从 1 ~ m 这些数组合成 n - m。
	2. 不包含m：count_partitions(n, m - 1)。因为不包含 m 这个数，所以 1 ~ m - 1 这些数要组合成n。
"""
def pre_largest_coin(coin):  # 获取前一个 coin
    if coin == 5:
        return 1
    elif coin == 10:
        return 5
    elif coin == 25:
        return 10
    
def cnt_coins(tot, cur_coin):
    if cur_coin == 1:  # 如果当前的 coin 是 1，那肯定只有一种情况 
        return 1
    pre_coin = pre_largest_coin(cur_coin)
    if tot < cur_coin:  # 如果当前的总量小于当前的 coin，就找前一个，即 pre_coin
        return cnt_coins(tot, pre_coin)
    return cnt_coins(tot, pre_coin) + cnt_coins(tot - cur_coin, cur_coin)  # 思路和 Refer 中的完全一样

def count_coins(total):
    return cnt_coins(total, 25)

# Q5
"""
only call expression, condition expression, lambda
no def, assignment
还不能调用 make_anonymous_factorial()
"""

Lecture 10 & 11

Textbook 2.2 Data Abstraction

2.2.1 & 2.2.2

由于浮点数有精度损失的问题，例如：1 / 3 == 0.333333333333333300000 is True，因此希望有某种方式来表示有理数，这里采用一个分母，一个分子来表示无理数，则上面的例子为：等号左边为：分子1，分母3，等号右边为：分子0.333333333333333300000，分母1。根据Chapter 1中将一系列运算抽象成函数的方法，我们首先假设已经实现了两个操作：1. 可以使用分子分母初始化一个有理数。2. 获取有理数的分子或者分母。这种假设很有用，可以暂时屏蔽底层的实现，更加关注运算层面的实现。

2.2.3 Abstraction Barriers

实现有理数的抽象过程中，我们可以分为三个大的部分：

  1. 有理数的运算：add_rational, mul_rational, print_rational等等，即对有理数的操作。
  2. 初始化有理数：rational, numer, denom。
  3. 有理数如何去存储。

可以作为分层的参考。

不好的抽象方式：

  1. add_rational([1, 2], [1, 4])，将1和2结合起来。

  2. def add_rational(x, y): return [x[0] * y[1] + x[1] * y[0], x[1] * y[1]]，将2和3结合起来。

Lab 04

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
# Q2
def skip_add(n):
    if n <= 2:
        return n
    else:
        return n + skip_add(n - 2)

# Q3
def summation(n, term):
    assert n >= 1
    if n == 1:
        return term(1)
    else:
        return term(n) + summation(n - 1, term)

# Q4
def paths(m, n):
    if m == 1 or n == 1:
        return 1
    return paths(m - 1, n) + paths(m, n - 1)

# Q5
def max_subseq(n, t):
    if len(str(n)) <= t:
        return n
    if t == 0:
        return 0
    elif t == 1:
        res, t_n = 0, n
        while t_n > 0:
            d = t_n % 10
            res = max(res, d)
            t_n //= 10
        return res
    else:
        a = max_subseq(n // 10, t)
        b = max_subseq(n // 10, t - 1)
        return max(a, b * 10 + n % 10)

# Q6
def add_chars(w1, w2):
    if len(w1) > len(w2):
        return
    if len(w1) == 0:
        return w2
    if w1[0] == w2[0]:
        return add_chars(w1[1:], w2[1:])
    else:
        return w2[0] + add_chars(w1, w2[1:])

Lecture 12 Trees

Textbook 2.3

讲的都是Sequence的语法，没仔细看。

Lecture 13 Binary Numbers (optional)

Lab 05

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
# Q1
def couple(s, t):
    assert len(s) == len(t)
    "*** YOUR CODE HERE ***"
    res = []
    for i in range(0, len(s)):
        res.append([s[i], t[i]])
    return res

# Q2
from math import sqrt
def distance(city_a, city_b):
    x1, y1 = get_lat(city_a), get_lon(city_a)
    x2, y2 = get_lat(city_b), get_lon(city_b)
    return sqrt((x1 - x2) ** 2 + (y1 - y2) ** 2)

# Q3
def closer_city(lat, lon, city_a, city_b):
    city_given = make_city('city_given', lat, lon)
    if (distance(city_given, city_a) < distance(city_given, city_b)):
        return get_name(city_a)
    else:
        return get_name(city_b)

# Q5
def berry_finder(t):
    """
    tree(label, branches=[])
    """
    if label(t) == None:
        return False
    elif label(t) == 'berry':
        return True
    else:
        branch = branches(t)
        for tree in branch:
            if berry_finder(tree):
                return True
        return False

# Q6
def sprout_leaves(t, leaves):
    if label(t) == None:
        return
    # 若leaves是一个[int]，则转化为[tree]
    if len(leaves) > 0 and isinstance(leaves[0], int):
        new_leaves = []
        for val in leaves:
            new_leaves.append(tree(val))
        leaves = new_leaves
    # 首先检查自己是不是叶子
    if is_leaf(t):
        t = tree(label(t), leaves)
        return t
    else:
        branch = branches(t)
        for i in range(len(branch)):
            branch[i] = sprout_leaves(branch[i], leaves)
        t = tree(label(t), branch)
        return t
    
# Q8
def coords(fn, seq, lower, upper):
    return [[x, fn(x)] for x in seq if fn(x) >= lower and fn(x) <= upper]

# Q9
def riffle(deck):
    """
    假设deck的长度为10，下标0~9(0~4, 5~9)，则访问的顺序应为：
    0, 5, 1, 6, 2, 7, 3, 8, 4, 9
    因此需要有如下的映射关系：
    0, 1, 2, 3, 4, 5, 6, 7, 8, 9
    |  |  |  |  |  |  |  |  |  |
    0, 5, 1, 6, 2, 7, 3, 8, 4, 9
    """
    return [deck[idx // 2 if idx % 2 == 0 else len(deck) // 2 + (idx - 1) // 2] for idx in range(len(deck))]

# Q10
def add_trees(t1, t2):
    if label(t1) == None:
        return t2
    if label(t2) == None:
        return t1
    branch1 = branches(t1)
    branch2 = branches(t2)
    if len(branch2) > len(branch1):
        branch1, branch2 = branch2, branch1
    len1, len2 = len(branch1), len(branch2)
    for i in range(len2):
        branch1[i] = add_trees(branch1[i], branch2[i])
    t1 = tree(label(t1) + label(t2), branch1)
    return t1

# Q11
def build_successors_table(tokens):
    """
    主要的目标就是找后继，直接看english这的不好理解。
    """
    table = {}
    prev = '.'
    for word in tokens:
        if prev not in table:
            "*** YOUR CODE HERE ***"
            table[prev] = [word]
        length = len(tokens)
        li = table[prev]
        for i in range(len(tokens)):
            if tokens[i] == prev and i != len(tokens) - 1 and tokens[i + 1] not in li:
                li.append(tokens[i + 1])
        "*** YOUR CODE HERE ***"
        prev = word
    return table

# Q12
def construct_sent(word, table):
    import random
    result = ''
    while word not in ['.', '!', '?']:
        "*** YOUR CODE HERE ***"
        result += ' ' + word
        next_word = table[word][0]  # 这里就不 random 了
        word = next_word

    return result.strip() + word

Lecture 14 Circuits

pass

Lecture 15 & 16 Mutable Values & Functions

Textbook 2.4

Adding state to data is a central ingredient of a paradigm called object-oriented programming.

Dictionaries: Tuples are commonly used for keys in dictionaries because lists cannot be used. ??

nonlocal: 我的理解就是，内部的函数可以使用外部的变量（即赋值的右边），但是不可以修改外部的变量，若需要修改则需要加上nonlocal关键字，来表明这个变量是外部的变量。



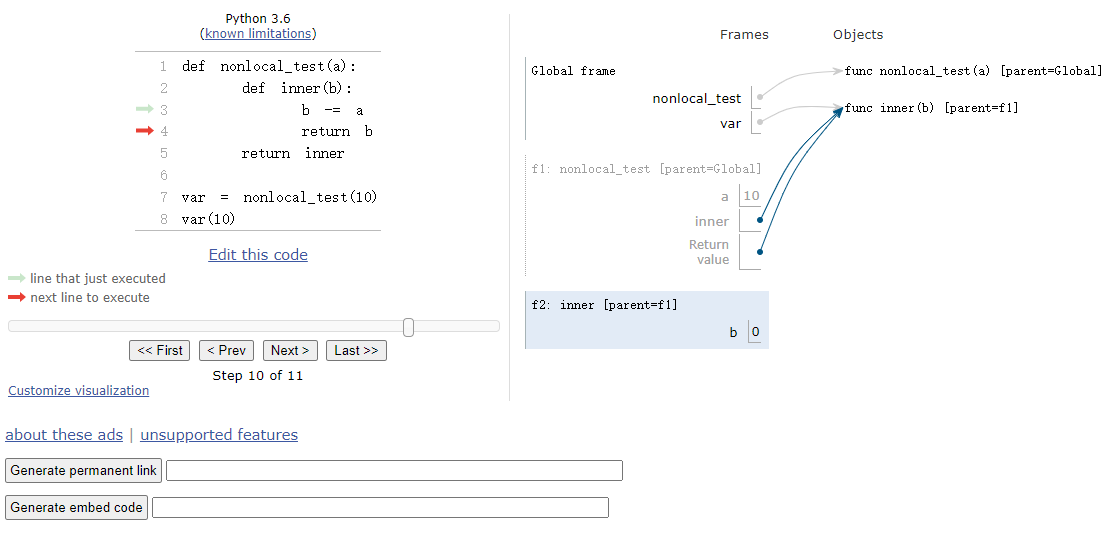
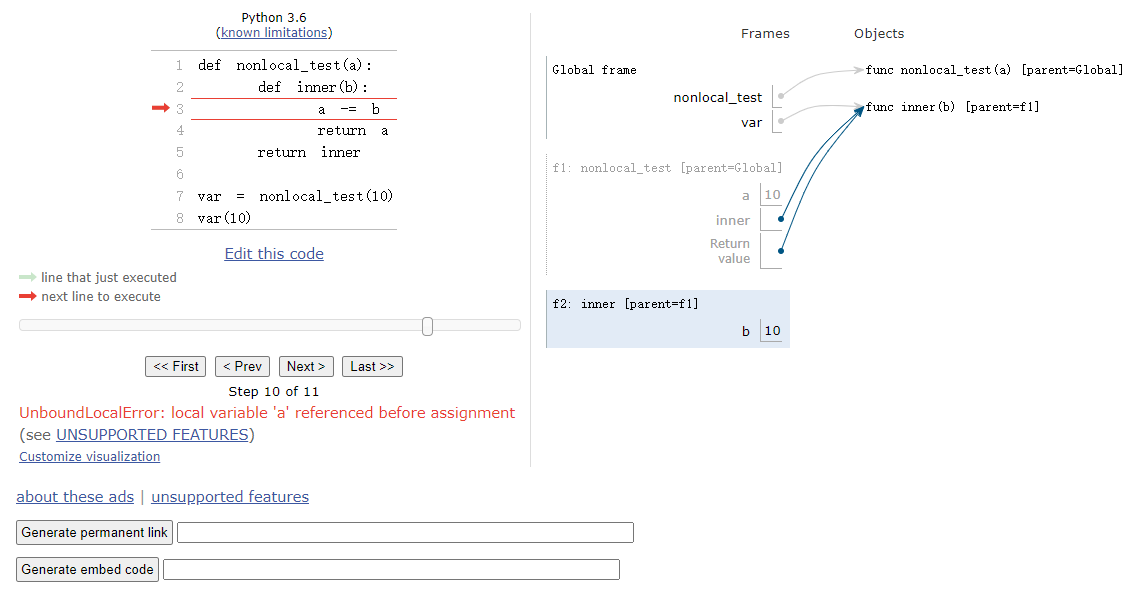
nonlocal的好处就是，可以维持内部的状态。貌似就是类中的属性，通过方法去修改它的值。

HW 03

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
# Q1
def planet(size):
    assert size > 0
    return ['planet', size]

def size(w):
    assert is_planet(w), 'must call size on a planet'
    return w[1] 

# Q2
def balanced(m):
    if not is_mobile(m):
        return False
    l, r = left(m), right(m)  # left or right
    l_m_or_p = end(l)  # left mobile or planet
    if is_mobile(l_m_or_p) and not balanced(l_m_or_p):
        return False
    r_m_or_p = end(r)
    if is_mobile(r_m_or_p) and not balanced(r_m_or_p):
        return False
    return length(l) * total_weight(l_m_or_p) == length(r) * total_weight(r_m_or_p)

# Q3
def totals_tree(m):
    # 1. 首先计算该节点的 weight，也就是 tree 的 label
    l, r = left(m), right(m)
    tot = total_weight(end(l)) + total_weight(end(r))
    # 2. 定义 tree 的 branch
    branch = []
    # 3. 若左边的节点是 mobile，递归调用 totals_tree，否则直接定义一个 tree 的节点
    if is_mobile(end(l)):
        branch.append(totals_tree(end(l)))
    else:
        branch.append(tree(total_weight(end(l))))
    # 4. 右边同理
    if is_mobile(end(r)):
        branch.append(totals_tree(end(r)))
    else:
        branch.append(tree(total_weight(end(r))))
    # 5. 返回这个 tree
    return tree(tot, branch)

# Q4
def replace_leaf(t, find_value, replace_value):
    new_t = copy_tree(t)
    if is_leaf(new_t):
        if label(new_t) == find_value:
            new_t[0] = replace_value
    elif is_tree(new_t):
        branch = branches(new_t)
        for i in range(len(branch)):
            branch[i] = replace_leaf(branch[i], find_value, replace_value)
        new_t = tree(label(new_t), branch)
    return new_t

# Q5
def preorder(t):
    res = [t[0]]
    for i in branches(t):
        res += preorder(i)
    return res

# Q6
def has_path(t, word):
    if label(t) != word[0]:
        return False
    if len(word) == 1:
        return True
    for node in branches(t):
        if has_path(node, word[1:]):
            return True
    return False

Lab 06

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
# Q1
def make_adder_inc(a):
    """
    与教程中的 withdraw 类似，t 作为一个需要维持的状态，
    一开始为 0，随着调用次数的增加，每次加 1。
    """
    t = -1
    def inner(b):
        nonlocal t
        t += 1
        return a + b + t
    return inner

# Q2
def make_fib():
    a, b = 0, 1
    first = True
    def inner():
        nonlocal a, b, first
        if first:
            first = False
        else:
            a, b = b, a + b
        return a
    return inner

# Q4
def insert_items(lst, entry, elem):
    length = len(lst)
    idx, cnt = 0, 0
    while cnt < length:
        if lst[idx] == entry:
            lst.insert(idx + 1, elem)
            idx += 2
        else:
            idx += 1
        cnt += 1
    return lst

Lecture 17 & 18 Iterators & Objects

HW 04

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
# Q1
def make_bank(balance):
    def bank(message, amount):
        "*** YOUR CODE HERE ***"
        nonlocal balance
        if message == 'withdraw':
            if amount > balance:
                return 'Insufficient funds'
            balance -= amount
            return balance
        elif message == 'deposit':
            balance += amount
            return balance
        else:
            return 'Invalid message'
    return bank

# Q2
def make_withdraw(balance, password):
    error_passwd_cnt = 0
    error_passwd_lst = []
    def withdraw(amount, passwd):
        nonlocal balance, error_passwd_cnt, error_passwd_lst
        if error_passwd_cnt == 3:
            return 'Frozen account. Attempts: ' + str(error_passwd_lst)
        if passwd != password:
            error_passwd_cnt += 1
            error_passwd_lst.append(passwd)
            return 'Incorrect password'
        # 感觉不是很合理，应该是有和这个 else 才比较符合逻辑的
        # else:
        #     error_passwd_cnt = 0
        if amount > balance:
            return 'Insufficient funds'
        balance -= amount
        return balance
    return withdraw

# Q3
def repeated(t, k):
    # 首先 t 是一个迭代器
    last, cnt = -1, 0  # 假设不可能为负数吧
    while True:
        try:
            x = next(t)
            if cnt == 0 or x != last:
                cnt = 1
            elif x == last:
                cnt += 1
            if cnt == k:
                cnt = 0
                return x
            last = x
        except:
            break
            
# Q4
def permutations_helper(lst):
    if len(lst) == 1:
        yield lst
    for i in range(len(lst)):  # 拿出一个元素
        x = lst[i]
        lst1 = lst[0 : i] + lst[i + 1 : ]
        for j in permutations_helper(lst1):
            yield [x] + j

def permutations(seq):
    lst = [v for v in seq]  # 存的就是需要排列的 seq
    return permutations_helper(lst)
上一页
2022-10-31 14:20:03 #Python #Awesome Courses
下一页